Where the techniques of Maths
are explained in simple terms.
Functions - Hyperbola.
Test Yourself 1 - Solutions.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| Basic hyperbolas. | 1. From the equation, there are asymptotes at x = 3 and y = 0. Draw these. There is no sign to reverse the x term. So a normal hyperbola.
|
2. From the equation, there are asymptotes at x = -2 and y = 0.
|
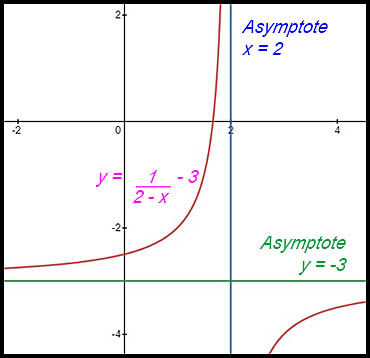
| 3. Subtracting the "2" from both sides gives y - 2 on the LHS so there is an asymptote at y - 2 = 0 or y = 2. Similarly there is an asymptote when the denominator x + 4 = 0 - so when x = -4. Draw these lines. The x term is positive so the hyperbola has its basic orientation.  |
4. Add the "3" to both sides gives Although there appears to be a + sign in front of the fraction, it is actually a negative when the terms are reversed. (i.e. -(x - 2)). So the hyperbola is flipped vertically. |
|
Determine the equation from a graph. |
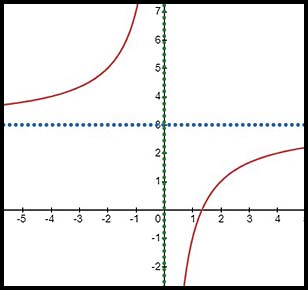
5. |
The curve is balanced on either side of the y axis and so there is no horizontal transformtion of the basic parabola. There is an asymptote at y = 1 so the hyperbola is shifted up 1. Hence the equation is:
|
6. 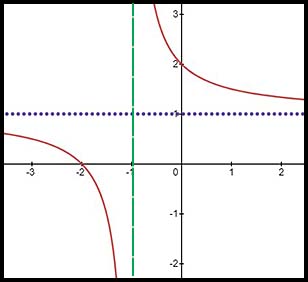 |
The shape of this graph is very similar to the shape of that in Q5. The asymptote at y = 1 is still there (so the equation must start Hence the equation is
|
|
7. 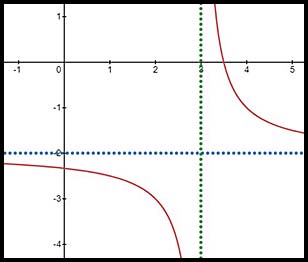 |
This hyperbola has been shifted from the basic position 3 units to the right and 2 units down. So write these shifts in terms of where the asymptotes are now: x = 3 and y = -2 Now rewrite as x - 3 = 0 and y + 2 = 0
|
|
8. 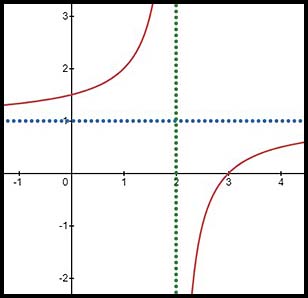 |
The basic hyperbola has been flipped vertically about the y axis and then shifted from its basic position 2 units to the right and 1 units up. So write these shifts in terms of where the asymptotes are now: x = 2 and y = 1. Then rewrite as x - 2 = 0 and y - 1 = 0 as usual.
|
|
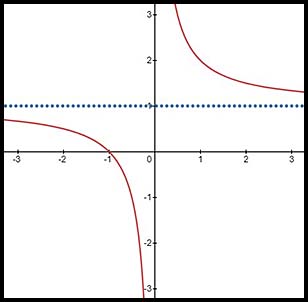
9. For the hyperbolic equation there are asymptotes when x - 1 = 0 - The absolute value leaves the RH arm of the hyperbola unaltered but the LH arm (which used negative values of y) is flipped around the x axis to become positive. |
|
|
10. For the hyperbolic equation 2x - 5 = 0 shows an asymptote at x = 2½ and y - 2 shows an asymptote at y = 2. Now draw it. (so the 2 in front of the x makes no difference to our technique). If there was a number greater than 1 in the numerator, that will simply push the arms away from the intersection of the asymptotes. How far can be determined by solving the equations for the axis intercepts. |
|
|
| More advanced hyperbolas | 11. (a) 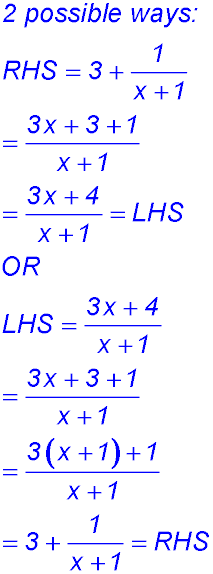
|
(b The equation can be analysed: x + 1 = 0 gives a vertical asymptote There is a positive sign in front of the fractional x term - so no flipping:
|
12. (a) Show that 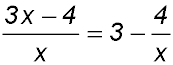
(b) Hence or otherwise, sketch a graph of |
(b) The x term has no number attached so the y axis is an asymptote. subtracting gives y - 3 on the left side so there is a horizontal asymptote at y = 3. The fractional x term is negative so the hyperbola is flipped vertically.
|
|
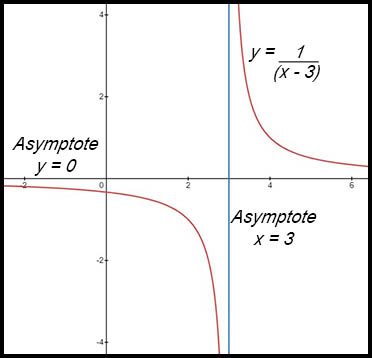
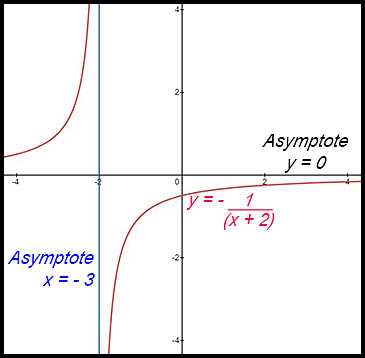
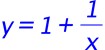
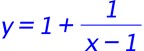
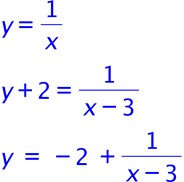

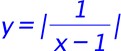 ,
,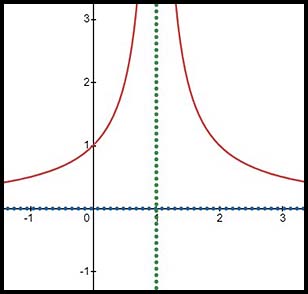
 , do nothing different to our standard procedure.
, do nothing different to our standard procedure.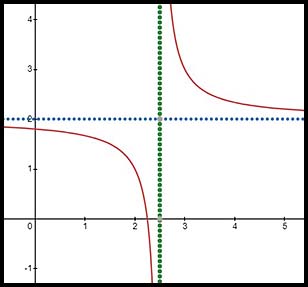

 Showing all important features.
Showing all important features.